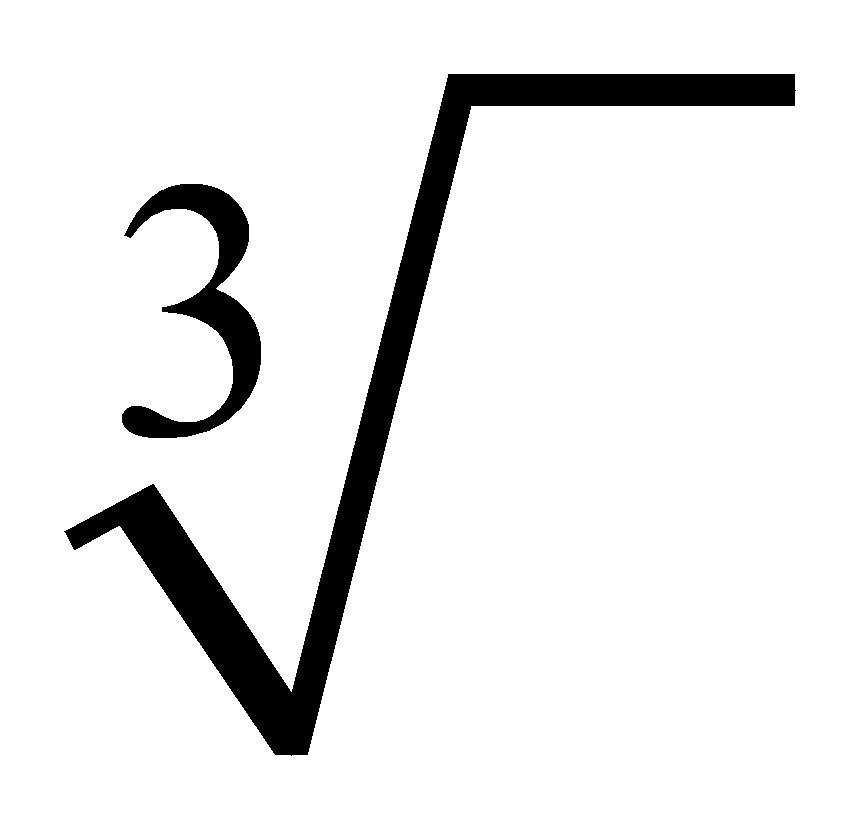segunda-feira, 19 de maio de 2014
POST FINAL
No início do ano, eu e minha turma 801 fizemos uma experiencia de cada um criar um blog para a aula de matemática do professor Emanuel Verçosa! A experiencia de ter criado um blog foi muito legal e me ajudou bastante a estudar matematica! Na verdade, eu olhava mais o blog do verçosa do que o meu próprio haha! é que ajudava muito! Toda vez que eu faltava a aula ou tinha alguma duvida, ele postava tudo no blog, era como se nós tivessemos um professor de matemática 24 horas por dia!! E também quando ele fez o hangout no youtube infelizmente eu nao pude parti- cipar por que era dia das mães.. mas depois quando fui estudar pra prova me ajudou muito e tirou muitas duvidas pela internet!! Quando eu criei o blog nao sabia direito sobre o que postar . . . mas ai o verçosa falou que podia ser qualquer coisa relacionado a matematica que nós pudessemos entender, entao fui pesquisando e postando no blog por causa desse trabalho que ele passou que é para o final do trimestre! é claro que não foi TÃÃÃÃÃAÃOOO facil assim de ter um blog... voce tem que sempre lembrar de postar e quando esquece tem que postar mais ainda........ e não é tao facil assim achar assuntos aleatórios sobre matemática!! Durante as aulas ele sempre para , pra tirar foto do quadro e postar no blog para que as pessoas que nao puderam estar presentes, conseguirem se adiantar com a matéria e a matéria é bem dificil então o site que o verçosa criou ajudou realmente muito todos os alunos..!!! ele na verdade é o unico professor que eu ja tive que criou um blog que me ajudou tanto assimm! e realmente foi muito legal e espero que ele continue postando no blog para tirar todas as nossas duvidas e muito mais... fazendo a matemática parecer ser uma coisa mais divertida e dar uma visão muito mais ampla sobre ela....! Muitas vezes eu nao tinha tempo de postar no blog e um dia eu estava olhando e vi que ele deixou um comentário para postar mais, entao comecei a postar mais desde aquele dia e meu site ficou com umas 10 publicações... enão é issoo..... essa foi a minha experiencia!! bjao
para quem perdeu o hangout do verçosa...
gente esse hangout me ajudou muito para estudar... espero que ajude vcs também!!
https://www.youtube.com/watch?v=KOBASjYWeCE
Quadriláteros
Pense bem um quadrilátero dividido diagonalmente formam 2 triangulos, e se a soma dos angulos de todo triangulo é 180, 180x2=360 que é a soma dos angulos internos de todo quadrilátero: TREZENTOS E SESSENTA.
.JPG)
angulos opostos pelo vertice
TODOS OS ANGULOS OPOSTOS PELO VÉRTICE SÃO """"""EXPLICITAMENTE"""""" IGUAIS
angulos de um triangulo
Todas as somas dos angulos internos de um triangulo é 180 graus! portanto nessa imagem X=55, pois 90+35= 125 e 180-125= 55
FATORAÇÃO
Definição de Fatoração
A fatoração é a transformação da soma e/ou subtração de vários termos em um produto de diversos fatores.
Vejamos alguns exemplos onde temos alguns dos principais tipos de fatoração:
Na sequência vemos como tratar cada um destes tipos de fatoração em particular.
A fatoração é um recurso que utilizamos na simplificação de sentenças matemáticas. Quando for o caso, podemos utilizá-la na simplificação de uma fração ou de uma equação, por exemplo.
MMC E MDC
O mínimo múltiplo comum, ou m.m.c., de dois ou mais números inteiros é o menor múltiplo inteiro positivo comum a todos eles. Por exemplo, o m.m.c. de 6 e 8 é o 24, e denotamos isso por mmc6, 8=24 Já o m.m.c. de 5, 6 e 8 é o 120, o que é denotado por mmc5, 6, 8=120.
O m.m.c. é muito útil quando se adicionam ou subtraem frações, pois é necessário um mesmo denominador comum durante esses processos. Não é necessário que esse denominador comum seja o m.m.c., mas a sua escolha minimiza os cálculos. Considere o exemplo:
326+18=656+756=1356, onde o denominador 56 foi usado porque mmc28, 8 = 56.
Regra prática para calcular o m.m.c. de dois números. Para calcular o m.m.c. entre 28 e 8, fazemos o seguinte:
1. Reduzimos a fração ,28-8. aos seus menores termos:
288=72.
2. Multiplicamos em cruz a expressão obtida:
28x2=8x7=56
3. O valor obtido é o m.m.c. procurado: mmc28, 8=56.
Regra geral para calcular o m.m.c. de dois ou mais números. O procedimento geral para o cálculo do m.m.c. envolve a decomposição primária de cada número. Por exemplo, para calcular o m.m.c. de 8, 12 e 28, fazemos o seguinte:
1. Realizamos a decomposição primária de cada número:
8=23
12=22∙31
28=22∙71
2. Em seguida, multiplicamos cada fator primo elevado à maior potência com que aparece nas fatorações. O resultado é o m.m.c. procurado:
mmc8, 12, 28=23∙31∙71=168
Dispositivo prático para calcular o m.m.c. de dois ou mais números. O procedimento acima tem a seguinte forma prática de execução:
1. Alinhamos os três números, 8, 12 e 28, e dividimos todos os números que podem ser divididos pelo primeiro primo 2. Na linha de baixo anotamos cada quociente obtido:
MMC e MDC (Foto: Colégio Qi)
2. Repetimos esse procedimento sucessivamente com o 2, depois com o 3 e, depois com o 7, até que a última linha só contenha algarismos 1:
MMC e MDC (Foto: Colégio Qi)
3. Agora, multiplicamos todos os fatores primos na coluna da direita, obtendo o m.m.c. procurado:
mmc8, 12, 28=2∙2∙2∙3∙7=168
PROPRIEDADE FUNDAMENTAL DO M.M.C. Todo múltiplo comum de dois ou mais números inteiros é múltiplo do m.m.c. destes números.
Exemplo: os múltiplos comuns positivos de 8, 12 e 28 são exatamente os múltiplos positivos de 168, o seu m.m.c., ou seja, são 168, 336, 504,...
Exemplo: encontre o menor número inteiro positivo de três algarismos que é divisível, ao mesmo tempo, por 3 ,4 e 15.
Solução: pela propriedade fundamental do m.m.c., o número desejado será o menor número de três algarismos múltiplo do m.m.c. de 3, 4 e 15. Como mmc3, 4, 15=60, então o menor múltiplo de três algarismos é o 120.
MÁXIMO DIVISOR COMUM (MDC)
O máximo divisor comum, ou m.d.c., de dois ou mais números inteiros é o maior divisor inteiro comum a todos eles. Por exemplo, o m.d.c. de 16 e 36 é o 4, e denotamos isso por mdc16,36=8. Já o m.d.c. de 30, 54 e 72 é o 6, o que é denotado por mdc30, 54, 72=6.
Regra geral para calcular o m.d.c. de dois ou mais números. O procedimento geral para o cálculo do m.d.c., como no caso do m.m.c., envolve a decomposição primária de cada número. Por exemplo, para calcular o m.m.c. de 30, 54 e 72, fazemos o seguinte:
1. Realizamos a decomposição primária de cada número:
30=21∙31∙51
36=22∙32
72=23∙32
2. Em seguida, multiplicamos os fatores primos comuns elevados à menor potência com que cada um aparece nas fatorações. O resultado é o m.d.c. procurado:
mmc30, 36, 72=21∙31=6
Dispositivo prático para calcular o m.d.c. de dois ou mais números. O procedimento acima tem a seguinte forma prática de execução:
1. Alinhamos os três números, 30, 36 e 72, e dividimos todos os números que podem ser divididos pelo primeiro primo 2. Na linha de baixo anotamos cada quociente obtido:
MMC e MDC (Foto: Colégio Qi)
2. Repetimos esse procedimento com o próximo primo que divida os três quocientes e, assim, sucessivamente, até que não hajam mais primos comuns:
MMC e MDC (Foto: Colégio Qi)
3. Agora, multiplicamos todos os fatores primos na coluna da direita, obtendo o m.d.c. procurado: mdc30, 36, 72=2∙3=6
O ALGORITMO DE EUCLIDES PARA O CÁLCULO DO M.D.C. DE DOIS NÚMEROS. Para o cálculo do m.d.c. de dois números, existe um dispositivo extremamente rápido e econômico. Trata-se do algoritmo de Euclides, que descrevemos, agora, para calcular o m.d.c. de 305 e 360.
1. Dividimos o maior número, 360, pelo menor, 305, obtendo resto 55, posicionando o resto abaixo do divisor:36030555
2. Em seguida, transportamos o resto 55 para o lado direito de 305 e dividimos o 305 por 55, posicionando o novo resto abaixo do 55:
Matemática (Foto: Reprodução)
3. Repetimos esse procedimento, transportando o novo resto 30 para o lado direito de 55 e dividimos o 55 por 30, posicionando o novo resto abaixo do 30. E continuamos assim, sucessivamente, até obter o primeiro resto 0:
Matemática (Foto: Reprodução)
4. O penúltimo resto obtido, ou seja, o resto anterior ao primeiro resto 0, é o m.d.c. dos dois números iniciais: mdc (305, 360) =resto anterior ao 0=5.
Números primos entre si ou primos relativos. Dois números inteiros são ditos primos entre si, ou primos relativos, se o m.d.c. entre eles é 1. É o caso de 10 e 21. Como mdc (10, 21) = 1, então 10 e 21 são primos entre si.
PROPRIEDADE FUNDAMENTAL DO M.D.C. Todo divisor comum de dois ou mais números inteiros é divisor do m.d.c. destes números.
Exemplo: 3 é divisor comum de 30, 36 e 72. Observe que 3 também é divisor de 6, o m.d.c. destes três números.
EXERCÍCIOS
1. (UEL) Três ciclistas percorrem um circuito saindo todos ao mesmo tempo, do mesmo ponto, e com o mesmo sentido. O primeiro faz o percurso em 40 s, o segundo em 36 s e o terceiro em 30 s.Com base nessas informações, depois de quanto tempo os três ciclistas se reencontrarão novamente no ponto de partida, pela primeira vez, e quantas voltas terá dado o primeiro, o segundo e o terceiro ciclistas, respectivamente?
(A) 5 minutos, 10 voltas, 11 voltas e 13 voltas.
(B) 6 minutos, 9 voltas, 10 voltas e 12 voltas.
(C) 7 minutos, 10 voltas, 11 voltas e 12 voltas.
(D) 8 minutos, 8 voltas, 9 voltas e 10 voltas.
(E) 9 minutos, 9 voltas, 11 voltas e 12 voltas.
Solução
O mmc30, 36,40 = 360 s=6min é o menor tempo em que os três se encontrarão novamente no ponto de partida. Por eliminação, já podemos marcar a letra B. Mas como encontrar o número de voltas de casa ciclista, basta dividir o tempo de 360 segundos pelo período de uma volta de cada um deles:
1o ciclista = 36040=9 voltas; 2o ciclista = 36036=10 voltas; 3o ciclista =36030=12 voltas
Resposta: letra B.
2. (PUC) “A Dengue é uma doença causada por um vírus, transmitida de uma pessoa doente para uma pessoa sadia por meio de um mosquito: o Aedes aegypti. Ela se manifesta de maneira súbita – com febre alta, dor atrás dos olhos e dores nas costas – e, como não existem vacinas específicas para o seu tratamento, a forma de prevenção é a única arma para combater a doença.”
Fonte (adaptado): prdu.unicamp.br/dengue/dengue.html
Assim sendo, suponha que 450 mulheres e 575 homens inscreveram-se como voluntários para percorrer alguns bairros do ABC paulista, a fim de orientar a população sobre os procedimentos a serem usados no combate à Dengue. Para tal, todas as 1.025 pessoas inscritas serão divididas em grupos, segundo o seguinte critério: todos os grupos deverão ter a mesma quantidade de pessoas e em cada grupo só haverá pessoas de um mesmo sexo. Nessas condições, se grupos distintos deverão visitar bairros distintos, o menor número de bairros a serem visitados é:
(A) 25
(B) 29
(C) 37
(D) 41
(E) 45
Solução
Quanto maior o número de pessoas em cada grupo, menor será o número total de grupos e, portanto, menor será o número de bairros visitados. Então, o número máximo de pessoas por grupo será o m.d.c. entre o número de homens e o número de mulheres, ou seja, mdc 450,575 = 25 pessoas por grupo. O número total de grupos será o número total de bairros visitados. Como temos 45025=18 grupos de mulheres e 57525=23 grupos de homens, teremos um total de 18+23=41 grupos e, portanto, 41 bairros visitados.
Resposta: letra D.
equação de 2 grau
Você sabe qual a diferença entre uma equação de 1º grau e uma de 2º? Está enganado quem achar que o nome tem a ver com ensino fundamental ou médio! O que determina o grau de uma equação é o expoente (a potência) da incógnita (a letra, geralmente x e y. Nas de 2º grau, o maior expoente da incógnita é 2.
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪13y2−7y=013x2=25x2+4x+10=34b2+25b+45=32b2+5−b
Existem equações de 3º grau, 4º grau etc. Por exemplo, a equação 6x + 5x⁴ + 45x² = 0 é uma equação do 4o grau, pois o maior expoente da incógnita x é 4.
Raízes da equação:
A solução de uma equação é chamada de raiz. O número de raízes possíveis de uma equação é igual ao seu grau. Equações de 2º grau possuem, então, no máximo duas raízes; equações de 3º grau possuem no máximo 3 raízes etc.
Equações de 2º grau incompletas
Algumas equações do 2º grau são de fácil solução:
Por exemplo: qual o número que elevado ao quadrado resulta 25?
Equacionando o problema:
x² = 25
Há dois números que satisfazem essa condição, ou há dois números que são raízes da equação (já que ela é de 2º grau).
Veja a resolução:
x =
±25√
X =
±5
5 e - 5 são raízes da equação de 2° grau x² = 25
Resolução de problemas com equações quadradas
Este é um problema clássico que pode ser resolvido por meio de equação de 2º grau incompleta.
Um homem quer construir uma casa de 8m por 10m. A legislação do município só permite construir, nesse loteamento, em no máximo máximo em 20% da área do terreno. Todos os terrenos são quadrados. Qual serão as medidas do terreno para construir a casa desejada?
A área do terreno é: Aterreno = x2
A área da casa é: Acasa = 8 . 10 = 80 m2
Como a área da casa será 20% da área do terreno, tem-se:
A área do terreno será Aterreno =
80.100?20?
= 400 m2
x2 = 400
x =
±400−−√
x =
±20
A raiz -20 é uma solução matemática do problema, mas não serve, pois a medida de um terreno não pode ser negativa. Logo, o terreno mede 20m de lado.
Veja outro problema: Qual o número que elevado ao quadrado e somado a 25 resulta zero?
Equacionando:
x2 + 25 = 0
x2 = - 25
Não existe um número que elevado ao quadrado que resulte em um número negativo.
A equação x2 + 25 = 0 não tem solução, ou não possui raízes no conjunto dos números reais, R.
Agora, vamos resolver a equação x 2 + 25x = 5x
Subtraindo 5x de ambos os lados:
x2 + 25x - 5x = 5x - 5x
x2 + 20x = 0
Colocando o x em evidência:
x (x + 20) = 0
Ora, se a multiplicação de dois números é igual a zero é porque pelo um deles é igual a zero.
⎧⎩⎨⎪⎪X?=0ou(X?+20)=0,?isto é,X?=−20
As raízes são zero e -20.
equações
Em matemática, uma equação é uma afirmação que estabelece uma igualdade entre duas expressões matemáticas.1 2
São exemplos de equações as seguintes igualdades:
x + 8 = 15
x^3 - 9x^2 - 7 = 4
3sen(x) + 25cos(x) = 18
3x^4 - x^3 + 5x^2 - 34x + 1211 = 0
tg(3y-25) + sen^3(cos(y^2 +4y -1))= 255
Nesses exemplos, as letras x e y são as incógnitas de suas equações. A incógnita de uma equação é o número desconhecido que se quer descobrir.
A equação x+8 = 15 pode ser interpretada como uma pergunta: "qual o número que somado com 8 dá 15?". Não é necessário nenhum método ou fórmula para encontrar o valor de x nesse caso: basta pensar um pouco para se chegar ao resultado x = 7.
Resolver uma equação é encontrar todos os valores possíveis para a incógnita que tornem a igualdade verdadeira.3 As equações mostradas nos exemplos acima podem ser interpretadas e resolvidas facilmente: o número que subtraído de 10 é igual a 4 é m = 6; o número que, ao ser multiplicado por 3, resulta em 18 é y=6.
Uma solução da equação também é chamada raiz da equação.
Algumas equações matemáticas descrevem, na verdade, identidades matemáticas, isto é, afirmações que são verdadeiras para todos os valores de x,2 como nos exemplos:
x(x+5) = x^2 + 5x
\mbox{sen}^2 x + \cos^2 x = 1
Entretanto, uma equação pode ter apenas alguns valores para os quais ela se torna verdadeira. Nesse caso, ela deve ser resolvida para se encontrar os valores possíveis para as incógnitas. Por exemplo, considere a equação:
x^2 - 3x = 0.
Ela é satisfeita para exatamente dois valores de x, a saber, x=0 e x=3.
Em geral, os matemáticos reservam a palavra equação exclusivamente para igualdades que não são identidades. A distinção entre esses dois conceitos pode ser bastante sutil. Por exemplo:
(x + 1)^2 = x^2 + 2x + 1
é uma identidade, mas:
(x + 1)^2 = 2x^2 + x + 1
é uma equação cujas soluções são x = 0 e x = 1.
Em geral, é possível perceber se se trata de uma identidade ou de uma equação pelo contexto em que a igualdade se encontra. Em alguns casos, na identidade, o sinal de igualdade (=) é trocado pelo sinal \equiv.
isaac newton um grande matematico
O trabalho de Newton foi descrito como "Um Trabalho distinto, que avançou cada destino da matemática". Sua obra sobre o assunto normalmente referido como cálculo, foi visto em um manuscrito no mês de Outubro de 1666, agora publicado entre os papéis matemáticos de Newton. A maioria dos historiadores modernos acreditam que Newton e Leibniz desenvolveram cálculo infinitesimal de forma independente, embora com diferentes notações. Ocasionalmente, tem sido sugerido que Newton publicou quase nada sobre isso até 1693, e não deu um relato completo até 1704, enquanto Leibniz começou a publicar um relato completo de seus métodos em 1684.(A Notação de Leibniz e o "Método diferencial", hoje reconhecidos como notações muito mais convenientes, foram adotados por matemáticos da Europa continental, e depois de 1820, também por matemáticos britânicos.) Esta sugestão, no entanto, não consegue explicar o conteúdo do cálculo que os críticos da época de Newton e dos tempos modernos têm apontado.
Mas o seu trabalho amplamente usa um cálculo infinitesimal em forma geométrica, com base em valores limite das proporções de pequenas quantidades: no Principia o próprio Newton deu uma demonstração sob o nome de "o método do primeiro e do último rácio" e explicou por que ele colocou as exposições desta forma.Devido a isso, o Principia foi chamado de "um livro denso com a teoria e aplicação do cálculo infinitesimal".
Newton tinha sido cauteloso em publicar o seu cálculo porque temia controvérsia e críticas. Ele era amigo do matemático suíço Nicolas Fatio de Duillier. Em 1691, Duillier começou a escrever uma nova versão de Principia e enviou a Leibniz. Em 1693, a relação entre Duillier e Newton acabou, e o livro nunca foi concluído.
A partir de 1699, outros membros da Royal Society (de que Newton era um membro) acusaram Leibniz de uma cópia fraudulenta, e a disputa surgiu com força total em 1711. A Royal Society proclamou em um estudo que foi Newton o verdadeiro descobridor e rotulou Leibniz de uma fraude. Este julgamento foi posto em dúvida quando se descobriu mais tarde que o próprio Newton escrevera considerações finais do estudo sobre Leibniz. Newton é creditado geralmente pelo binómio de Newton, válido para qualquer expoente, descobriu as identidades de Newton, o Método de Newton, fez contribuições substanciais para a teoria do operador de diferença, e foi o primeiro a usar índices fracionários para empregar na geometria para obter soluções para a equaçã. Newton foi nomeado Professor lucasiano de Matemática ,em 1669, por recomendação de Isaac Barrow.
dizimasss!!!!!!
Uma dízima periódica é um número que quando escrito no sistema decimal apresenta uma série infinita de algarismos decimais que, a partir de um certo algarismo, se repetem em grupos de um ou mais algarismos, ordenados sempre na mesma disposição e chamados de período
Numa dízima periódica simples, o período aparece imediatamente após a vírgula.
Exemplos:
0,444444…
0,5125125125…
0,68686868…
Na dízima periódica composta, há um ou mais algarismos entre a vírgula e o período, que não entram na composição do período.
Exemplos:
0,72222222…
0,58444444…
Toda dízima periódica representa um numero racional, isto é justificado de forma construtiva, ou seja, encontrando a fração que dá origem à dízima.
NUMEROS:
NATURAIS -> EX; 1+1=2
INTEIROS ->OS NUMEROS POSITIVOS E NEGATIVOS EX;... -4_-3_-2_-1_0_1 2 3 4...
RACIONAIS -> FRACOES EX; 1/2, 4/3 ...
IRRACIONAIS -> NAO PODEM FORMAR FRACAO EX: RAIZ QUADRADA DE 7,2..
REAIS -> TODOS ACIMA
.
OPERACOES COM OS REAIS:
<3 ASSOCIATIVIDADE -> QUANDO A OPERACAO E A MESMA, E O PARENTESES MUDA DE ORDEM , NAO ALTERA O RESULTADO.
EX: A+(B+C)=
(A+B)+C =
<3 COMUTATIVIDADE:
QUANDO A OPERACAO E A MESMA, E OS NUMEROS MUDAM DE ORDEM , NAO ALTERA O RESULTADO.
EX; A+B=B+A
<3 ELEMENTO NEUTRO
ADICAO=ZERO MULTIPLICACAO=UM
<3 ELEMENTO OPOSTO
EX; 2=-2
<3 ELEMENTO INVERSO
EX; 2=1/2
<3 DISTRIBUTIVA
EX: A(B+C)=AB+AC
é muito dificil explicar o que é uma RETA...
Em matemática, uma reta (AO 1945: recta) é um objeto geométrico infinito a uma dimensão. Trata-se da menor distância imaginável entre dois pontos distintos.1 [nota 1] No texto original de Os Elementos, de Euclides, fala-se de segmento de reta e não de retas.
Afinal... o que são angulos??
Ângulo é a região de um plano concebida pelo encontro de duas semirretas que possuem uma origem em comum, chamada vértice do ângulo1 . A abertura do ângulo é uma propriedade invariante e é medida em radianos ou graus. Ângulo é um dos conceitos fundamentais da matemática, ocupando lugar de destaque na Geometria euclidiana, ao lado de ponto, reta, plano, triângulo, quadrilátero, polígono e perímetro2 .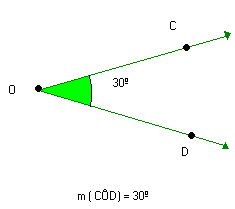
inequação
Inequação: toda a desigualdade literal que é apenas satisfeita por certos valores, as letras ou incongnitas que nela figuram, por outras palavras, apresentam os sinais de maior (>) ou menor (<) ao invês do sinal de igualdade que é o caracteriza as equações.
Soluçoes ou Raízes de uma Inequação: os valores das incógnitas ou letras que satisfazem a inequação, que a transformam numa desigualdade nemerica.
esses são exemplos de inequações:
juros simples
O regime de juros será simples quando o percentual de juros incidir apenas sobre o valor principal. Sobre os juros gerados a cada período não incidirão novos juros. Valor Principal ou simplesmente principal é o valor inicial emprestado ou aplicado, antes de somarmos os juros. Transformando em fórmula temos:
J = P . i . n
J = juros
P = principal (capital)
i = taxa de juros
n = número de períodos Exemplo: Temos uma dívida de R$ 1000,00 que deve ser paga com juros de 8% a.m. pelo regime de juros simples e devemos pagá-la em 2 meses. Os juros que pagarei serão:
J = 1000 x 0.08 x 2 = 160
Ao somarmos os juros ao valor principal temos o montante.
Montante = Principal + Juros
Montante = Principal + ( Principal x Taxa de juros x Número de períodos )
M = P . ( 1 + ( i . n ) )
Exemplo: Calcule o montante resultante da aplicação de R$70.000,00 à taxa de 10,5% a.a. durante 145 dias.
SOLUÇÃO:
M = P . ( 1 + (i.n) )
M = 70000 [1 + (10,5/100).(145/360)] = R$72.960,42
Observe que expressamos a taxa i e o período n, na mesma unidade de tempo, ou seja, anos. Daí ter dividido 145 dias por 360, para obter o valor equivalente em anos, já que um ano comercial possui 360 dias.
raiz cubica
Oo que mais ouvimos falar é a raiz quadrada, mas para fazer a raiz cubica é quase o mesmo, só que ao invez de juntar apenas 2 numeros na fatoração, voce junta 3!! uma imagem da representação de uma raiz cubica:
Hipotenusa
O Teorema de Pitágoras é considerado uma das principais descobertas da Matemática, ele descreve uma relação existente no triângulo retângulo. Vale lembrar que o triângulo retângulo pode ser identificado pela existência de um ângulo reto, isto é, medindo 90º. O triângulo retângulo é formado por dois catetos e a hipotenusa, que constitui o maior segmento do triângulo e é localizada oposta ao ângulo reto..jpg)
potencias...
Definição
Dado um certo número real qualquer, e um número n, inteiro e positivo, é definido in = potência de base (i) e com expoente (n) como sendo o produto de n fatores iguais a (i).
Exemplos de fixação da definição:
Potência = 23
2 x 2 x 2 = ( 03 fatores) = 8
Potência = 35
3 x 3 x 3 x 3 x 3 = (05 fatores) = 243
Notação: 23 = 8
2 - BASE
3 - EXPOENTE
8 - POTÊNCIA
Notação: 35 = 243
3 - BASE
5 - EXPOENTE
243 - POTÊNCIA
Alguns casos particulares:
1) Expoente igual a um (1)
(1/2)1 = 1/2
51 = 5
31 = 3
2) Expoente igual à zero (0)
50 = 1
60 = 1
70 = 1
Por convenção, resolveu-se que toda número elevado ao número zero, o resultado será igual a 1.
Mais Exemplos de fixação da definição:
1) 53 = 5 x 5 x 5 = 125
2) 40 = 1
3) 100 = 1
4) 201 = 20
MAGICAA!
Peça para a pessoa, com uma calculadora:
1º) Digitar os 4 primeiros números de telefone dela;
2º) Multiplicar por 80;
3º) Somar 1;
4º) Multiplicar por 250;
5º) Somar os 4 últimos números do telefone dela;
6º) Somar mais uma vez os 4 últimos números do telefone dela;
7º) Subtrair 250;
8º) Dividir 2.
O resultado será o telefone dessa pessoa!
desafioo!!!!!
Desafio 1: Acompanhe o raciocínio
homens
muro
dias
2
1
3
10
5
?
Temos 10 homens para construir 5 muros e sabemos que 2 homens gastam 3 dias para construir um muro. Se separarmos os 10 homens em duplas, teremos 5 duplas. Se cada dupla ficar responsável por um muro, teremos a seguinte situação:
Se todas as duplas começarem o trabalho no mesmo momento, cada uma concluirá o seu respectivo muro ao final de 3 dias, pois 2 homens gastam 3 dias para construir um muro, e como as duplas começaram juntas, terminarão juntas. Ou seja, 10 homens levam 3 dias para construir 5 muros.
:)
Desafio 2. Esse desafio foca a atenção na leitura e interpretação dos dados. Observe que na propriedade havia 50 bois e 100 vacas. No dia do incidente morreram 15 vacas. A questão a ser respondida é: ”Quantos bois restaram após o incidente?” Note que nenhum boi morreu. Apenas vacas. Portanto, restaram os 50 bois que haviam inicialmente.
:)
desafio 3. Esse desafio é uma “brincadeira” para ser feita com colegas ou familiares. É necessário o uso de uma calculadora para realizar os cálculos com rapidez.
Suponha que a idade de seu colega seja 12 anos:
12 x 2 = 24
24 + 10 = 34
34 x 50 = 1700
Suponhamos que a família dele seja composta por 5 pessoas:
1700 + 5 = 1705
1705 – 500 =1205
Através do número 1205 concluímos que sua idade é 12 anos e que em sua família há 05 pessoas.
monomios
Monômios
Monômio ou termo algébrico é toda expressão algébrica determinada por apenas um número real, uma variável ou pelo produto de números e variáveis.
Monômios
Não Monômios
Partes de um monômio
Um monômio é dividido em duas partes, um número, que é o coeficiente do monômio e uma variável ou o produto devariáveis (letras), inclusive suas potências, caso existam.
2x → 2 é o coeficiente desse monômio e x é sua parte literal;
3xy2 → 3 é o coeficiente desse monômio e xy2 é sua parte literal;
wz → 1 é o coeficiente desse monômio e wz é sua parte literal.
Grau de um monômio
Para um monômio com coeficientes não nulos, temos que seu grau se dará através da soma entre os expoentes da parte literal.
1/2x2y3z4 → esse é um monômio do 9º grau (2 + 3 + 4 = 9);
bcd → esse é um monômio do 3º grau (1 + 1 + 1+ = 3).
25 → esse é um monômio de grau zero (ausência da parte literal);
Entre os monômios 2x2, 1/3x3 e 0,5x5 o de maior grau é 0,5x5, pois 5 > 2 > 1/3.
Pode-se também atribuir o grau de um monômio em relação a uma de suas incógnitas. Para isso é necessário fazer menção a incógnita considerada. Vejam nos exemplos:
ab2 → esse é um monômio do 2º grau em relação a variável b;
wz3 → esse é um monômio do 1º grau em relação a variável w;
4 → esse é um monômio de grau zero pela ausência de variável (eis).
Semelhança entre monômios
Dois ou mais monômios são semelhantes quando suas partes literais são iguais.
3xy e 2/5xy são iguais, pois possuem a mesma parte literal xy;
0,5a3b2 e 10a3b2 são iguais, pois possuem a mesma parte literal a3b2;
- 4vwz, 2,3vwz e 1/3vwz são iguais, pois possuem a mesma parte literal vwz.
Adicionando e/ou subtraindo monômios
Na adição de monômios com a mesma parte literal, adicionaremos os coeficientes entre si e manteremos a parte literal.
2mn + 14mn + 5mn = 21mn (2 + 14 + 5 = 21);
2,5 x2y + 1,5x2y – 0,5x2y = 3,5x2y (2,5 + 1,5 – 0,5 = 3,5);
3/2cd3 – 1/2cd3 + 5/2cd3 = 7/2cd3 (3/2 – 1/2 + 5/2 = 7/2).
Um refrigerante custa x reais. Márcio comprou 3 refrigerantes, Aline comprou 2, Poliana comprou 4 e Arthur comprou 1. Qual é o monômio que representa quanto essas pessoas gastaram? → 3 + 2 + 4 + 1 = 10, portanto 10x.
sábado, 17 de maio de 2014
Assinar:
Postagens (Atom)